On Compatible Matchings

O. Aichholzer, A. Arroyo, Z. Masárová, I. Parada, D. Perz, A. Pilz, J. Tkadlec, and B. Vogtenhuber

Abstract:

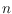
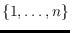
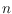
A matching is compatible to two or more labeled point sets of size $n$ with labels $\{1,\dots,n\}$ if its straight-line drawing on each of these point sets is crossing-free. We study the maximum number of edges in a matching compatible to two or more labeled point sets in general position in the plane. 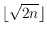We show that for any two labeled convex sets of $n$ points there exists a compatible matching with $\lfloor \sqrt {2n}\rfloor$ edges. More generally, for any $\ell$ labeled point sets we construct compatible matchings of size $\Omega(n^{1/\ell})$. 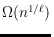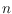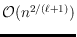As a corresponding upper bound, we use probabilistic arguments to show that for any $\ell$ given sets of $n$ points there exists a labeling of each set such that the largest compatible matching has $\mathcal{O}(n^{2/(\ell+1)})$ edges. 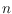Finally, we show that $\Theta(\log n)$ copies of any set of $n$ points are necessary and sufficient for the existence of a labeling such that any compatible matching consists only of a single edge.

Reference: O. Aichholzer, A. Arroyo, Z. Masárová, I. Parada, D. Perz, A. Pilz, J. Tkadlec, and B. Vogtenhuber. On compatible matchings. Journal of Graph Algorithms and Applications, 26(2):225-240, 2022.