Disjoint compatibility graph of non-crossing matchings of points in convex position

O. Aichholzer, A. Asinowski, and T. Miltzow

Abstract:

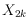
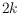
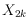
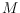
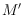
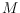
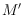
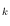
Let $X_{2k}$ be a set of $2k$ labeled points in convex position in the plane. We consider geometric non-intersecting straight-line perfect matchings of $X_{2k}$. Two such matchings, $M$ and $M'$, are disjoint compatible if they do not have common edges, and no edge of $M$ crosses an edge of $M'$. Denote by $\dcm_k$ the graph whose vertices correspond to such matchings, and two vertices are adjacent if and only if the corresponding matchings are disjoint compatible. 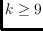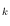We show that for each $k \geq 9$, the connected components of $\dcm_k$ form exactly three isomorphism classes - namely, there is a certain number of isomorphic small components, a certain number of isomorphic medium components, and one big component. The number and the structure of small and medium components is determined precisely.

Reference: O. Aichholzer, A. Asinowski, and T. Miltzow. Disjoint compatibility graph of non-crossing matchings of points in convex position. The Electronic Journal of Combinatorics, 22:1-65, 2015.