Progress on rectilinear crossing numbers

O. Aichholzer, F. Aurenhammer, and H. Krasser

Abstract:

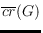
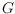
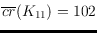
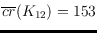
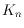
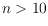
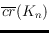
Let $\overline{cr}(G)$ denote the rectilinear crossing number of a graph $G$. We show $\overline{cr}(K_{11})=102$ and $\overline{cr}(K_{12})=153$. Despite the remarkable hunt for the crossing number of the complete graph $K_n$, initiated by R. Guy in the 1960s, these quantities have been unknown for $n>10$ to date. 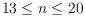We also establish new upper and lower bounds on $\overline{cr}(K_{n})$ for $13 \leq n \leq 20$, along with an improved general lower bound for $\overline{cr}(K_{n})$. 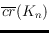The results mainly rely on recent methods developed by the authors for exhaustively enumerating all combinatorially inequivalent sets of points (so-called order types).

Reference: O. Aichholzer, F. Aurenhammer, and H. Krasser. Progress on rectilinear crossing numbers. Technical report, IGI-TU Graz, Austria, 2002.