Improved Upper Bounds on the Reflexivity of Point Sets

E. Ackerman, O. Aichholzer, and B. Keszegh

Abstract:

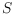
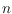
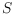
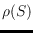
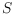
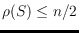
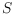
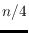
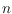
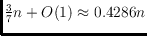
Given a set $S$ of $n$ points in the plane, the reflexivity of $S$, $\rho(S)$, is the minimum number of reflex vertices in a simple polygonalization of $S$. Arkin et al. proved that $\rho(S) \le n/2$ for any set $S$, and conjectured that the tight upper bound is $n/4$. We show that the reflexivity of any set of $n$ points is at most $\frac{3}{7}n + O(1) \approx 0.4286n$. 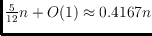Using computer-aided abstract order type extension the upper bound can be further improved to $\frac{5}{12}n + O(1) \approx 0.4167n$.

Reference: E. Ackerman, O. Aichholzer, and B. Keszegh. Improved upper bounds on the reflexivity of point sets. Computational Geometry: Theory and Applications, 42:241-249, 2009.