On the Crossing Number of Complete Graphs - Extended Abstract

O. Aichholzer, F. Aurenhammer, and H. Krasser

Abstract:

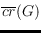
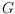
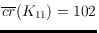
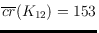
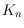
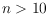
Let $\overline{cr}(G)$ denote the rectilinear crossing number of a graph $G$. We determine $\overline{cr}(K_{11})=102$ and $\overline{cr}(K_{12})=153$. Despite the remarkable hunt for crossing numbers of the complete graph $K_n$ - initiated by R. Guy in the 1960s - these quantities have been unknown for $n>10$ to date. Our solution mainly relies on a tailor-made method for enumerating all inequivalent sets of points (so-called order types) of size $11$. 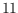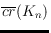Based on these findings, we establish new upper and lower bounds on $\overline{cr}(K_{n})$ for general $n$. 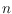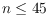Specific values for $n \leq 45$ are given, along with significantly improved asymptotic values. 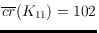The asymptotic lower bound is immediate from the fact $\overline{cr}(K_{11})=102$, whereas the upper bound stems from a novel construction of drawings with few crossings. The construction is shown to be optimal within its frame. 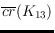The tantalizing question of determining $\overline{cr}(K_{13})$ is left open. 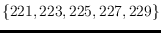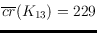The latest ra(n)ge is $\{221,223,225,227,229\}$; our conjecture is $\overline{cr}(K_{13}) = 229$.

Reference: O. Aichholzer, F. Aurenhammer, and H. Krasser. On the crossing number of complete graphs - extended abstract. In Proc. $18^{th}$ European Workshop on Computational Geometry CG '02 Warszawa, pages 90-92, Warszawa, Poland, 2002.