Generalized self-approaching curves

O. Aichholzer, F. Aurenhammer, C. Icking, R. Klein, E. Langetepe, and G. Rote

Abstract:

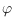
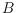
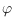
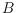
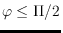
We consider all planar oriented curves that have the following property depending on a fixed angle $\varphi$. For each point $B$ on the curve, the rest of the curve lies inside a wedge of angle $\varphi$ with apex in $B$. This property restrains the curve's meandering, and for $\varphi \leq \Pi/2$ this means that a point running along the curve always gets closer to all points on the remaining part. 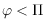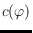For all $\varphi < \Pi$, we provide an upper bound $c(\varphi)$ for the length of such a curve, divided by the distance between its endpoints, and prove this bound to be tight. 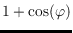A main step is in proving that the curve's length cannot exceed the perimeter of its convex hull, divided by $1+\cos(\varphi)$.

Reference: O. Aichholzer, F. Aurenhammer, C. Icking, R. Klein, E. Langetepe, and G. Rote. Generalized self-approaching curves. In Proc. $9^{th}$ Int. Symp. Algorithms and Computation ISAAC'98, Lecture Notes in Computer Science, volume 1533, pages 317-326, Taejon, Korea, 1998. Springer Verlag.