An improved lower bound on the number of triangulations

O. Aichholzer, V. Alvarez, T. Hackl, A. Pilz, B. Speckmann, and B. Vogtenhuber

Abstract:

Upper and lower bounds for the number of geometric graphs of specific types on a given set of points in the plane have been intensively studied in recent years. For most classes of geometric graphs it is now known that point sets in convex position minimize their number. However, it is still unclear which point sets minimize the number of geometric triangulations; the so-called double circles are conjectured to be the minimizing sets. 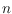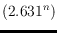In this paper we prove that any set of $n$ points in general position in the plane has at least $\Omeag(2.631^n)$ geometric triangulations. 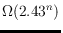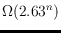Our result improves the previously best general lower bound of $\Omega(2.43^n)$ and also covers the previously best lower bound of $\Omega(2.63^n)$ for a fixed number of extreme points. We achieve our bound by showing and combining several new results, which are of independent interest: 1. 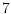Adding a point on the second convex layer of a given point set (of $7$ or more points) at least doubles the number of triangulations. 2. Generalized configurations of points that minimize the number of triangulations have at most ${[}n/2{]}$ points on their convex hull. 3. We provide tight lower bounds for the number of triangulations of point sets with up to 15 points. These bounds further support the double circle conjecture.

Reference: O. Aichholzer, V. Alvarez, T. Hackl, A. Pilz, B. Speckmann, and B. Vogtenhuber. An improved lower bound on the number of triangulations. In Proc. $32^{nd}$ Int. Sympos. Comput. Geom. (SoCG) volume 51 of Leibniz International Proceedings in Informatics (LIPIcs), pages 7:1-7:16, Boston, USA, 2016.