Recovering Structure from r-Sampled Objects

O. Aichholzer, F. Aurenhammer, B. Kornberger, S. Plantinga, G. Rote, A. Sturm, and G. Vegter

Abstract:

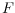
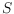
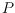
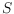
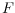
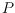
For a surface $F$ in 3-space that is represented by a set $S$ of sample points, we construct a coarse approximating polytope $P$ that uses a subset of $S$ as its vertices and preserves the topology of $F$. In contrast to surface reconstruction we do not use all the sample points, but we try to use as few points as possible. 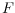Such a polytope $P$ is useful as a `seed polytope' for starting an incremental refinement procedure to generate better and better approximations of $F$ based on interpolating subdivision surfaces or e.g. Bézier patches. 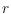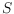Our algorithm starts from an $r$-sample $S$ of $F$. 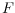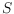Based on $S$, a set of surface covering balls with maximal radii is calculated such that the topology is retained. 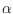From the weighted $\alpha$-shape of a proper subset of these highly overlapping surface balls we get the desired polytope. As there is a rather large range for the possible radii for the surface balls, the method can be used to construct triangular surfaces from point clouds in a scalable manner. We also briefly sketch how to combine parts of our algorithm with existing medial axis algorithms for balls, in order to compute stable medial axis approximations with scalable level of detail.

Reference: O. Aichholzer, F. Aurenhammer, B. Kornberger, S. Plantinga, G. Rote, A. Sturm, and G. Vegter. Recovering structure from r-sampled objects. In Eurographics Symposium on Geometry Processing, special issue of Computer Graphics Forum 28(5), pages 1349-1360, Berlin, Germany, 2009.