Transforming Spanning Trees and Pseudo-Triangulations

O. Aichholzer, F. Aurenhammer, C. Huemer, and H. Krasser

Abstract:

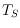
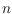
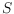
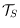
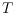
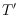
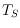
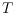
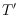
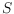
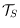
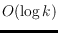
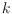
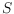
Let $T_{S}$ be the set of all crossing-free straight line spanning trees of a planar $n$-point set $S$. Consider the graph ${\cal T}_S$ where two members $T$ and $T'$ of $T_{S}$ are adjacent if $T$ intersects $T'$ only in points of $S$ or in common edges. We prove that the diameter of ${\cal T}_S$ is $O(\log k)$, where $k$ denotes the number of convex layers of $S$. 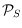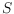Based on this result, we show that the flip graph ${\cal P}_S$ of pseudo-triangulations of $S$ (where two pseudo-triangulations are adjacent if they differ in exactly one edge - either by replacement or by removal) has a diameter of $O(n \log k)$. 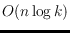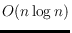This sharpens a known $O(n \log n)$ bound. 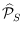Let  ${\cal \widehat{P}}_S$ be the induced subgraph of pointed pseudo-triangulations of ${\cal P}_S$. 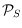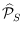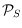We present an example showing that the distance between two nodes in  ${\cal \widehat{P}}_S$ is strictly larger than the distance between the corresponding nodes in ${\cal P}_S$.

Reference: O. Aichholzer, F. Aurenhammer, C. Huemer, and H. Krasser. Transforming spanning trees and pseudo-triangulations. In Proc. $21^{th}$ European Workshop on Computational Geometry EWCG '05, pages 81-84, Eindhoven, The Nederlands, 2005.