O. Aichholzer, F. Aurenhammer, F. Hurtado, and H. Krasser
We state the following conjecture: any two planar
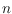
-point sets (that agree on
the number of convex hull points) can be triangulated in a compatible manner,
i.e., such that the resulting two triangulations are topologically
equivalent. The conjecture is proved true for point sets with at most three
interior points. We further exhibit a class of point sets which can be
triangulated compatibly with any other set that satisfies the obvious size
and hull restrictions. Finally, we prove that adding a small number of
extraneous points (the number of interior points minus two) always allows for
compatible triangulations.