Computational and Structural Advantages of Circular Boundary
Representation
O. Aichholzer, F. Aurenhammer, T. Hackl, B. Jüttler, M. Oberneder,
and Z. Sír
Abstract:
Boundary approximation of planar shapes by circular arcs has quantitive and
qualitative advantages compared to using straight-line segments. We
demonstrate this by way of three basic and frequent computations on shapes -
convex hull, decomposition, and medial axis. In particular, we propose a
novel medial axis algorithm that beats existing methods in simplicity and
practicality, and at the same time guarantees convergence to the medial axis
of the original shape.
Reference: O. Aichholzer, F. Aurenhammer, T. Hackl, B. Jüttler,
M. Oberneder, and Z. Sír.
Computational and structural advantages of circular boundary representation.
In Lecture Notes in Computer Science (LNCS), Proc. 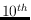 International Workshop on Algorithms and Data Structures (WADS), volume
4619, pages 374-385, Halifax, Nova Scotia, Canada, 2007.
International Workshop on Algorithms and Data Structures (WADS), volume
4619, pages 374-385, Halifax, Nova Scotia, Canada, 2007.
www-data,
2020-09-10