On $k$-Convex Point Sets

O. Aichholzer, F. Aurenhammer, T. Hackl, F. Hurtado, A. Pilz, P. Ramos, J. Urrutia, P. Valtr, and B. Vogtenhuber

Abstract:

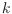
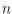
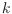
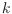
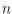
We extend the (recently introduced) notion of $k$-convexity of a two-dimensional subset of the Euclidean plane to finite point sets. A set of $n$ points is considered $k$-convex if there exists a spanning (simple) polygonization such that the intersection of any straight line with its interior consists of at most $k$ disjoint intervals. 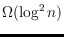As the main combinatorial result, we show that every $n$-point set contains a subset of $\Omega(\log^2 n)$ points that are in 2-convex position. This bound is asymptotically tight. 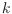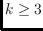From an algorithmic point of view, we show that 2-convexity of a finite point set can be decided in polynomial time, whereas the corresponding problem on $k$-convexity becomes NP-complete for any fixed $k\geq 3$.

Reference: O. Aichholzer, F. Aurenhammer, T. Hackl, F. Hurtado, A. Pilz, P. Ramos, J. Urrutia, P. Valtr, and B. Vogtenhuber. On $k$-convex point sets. Computational Geometry: Theory and Applications, 47(8):809-832, 2014.