Connecting Colored Point Sets

O. Aichholzer, F. Aurenhammer, T. Hackl, and C. Huemer

Abstract:

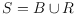
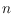
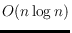
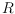
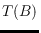
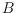
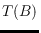
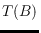
We study the following Ramsey-type problem. Let $S = B \cup R$ be a two-colored set of $n$ points in the plane. We show how to construct, in $O(n \log n)$ time, a crossing-free spanning tree $T(R)$ for $R$, and a crossing-free spanning tree $T(B)$ for $B$, such that both the number of crossings between $T(R)$ and $T(B)$ and the diameters of $T(R)$ and $T(B)$ are kept small. The algorithm is conceptually simple and is implementable without using any non-trivial data structure. This improves over a previous method in Tokunaga [#!T!#] that is less efficient in implementation and does not guarantee a diameter bound.

Reference: O. Aichholzer, F. Aurenhammer, T. Hackl, and C. Huemer. Connecting colored point sets. Discrete Applied Mathematics, 155(3):271-278, 2007.