Sequences of spanning trees and a fixed tree theorem

O. Aichholzer, F. Aurenhammer, and F. Hurtado

Abstract:

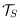
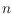
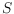
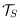
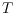
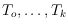
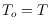
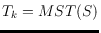
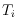
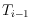
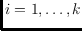
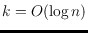
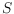
Let ${\cal T}_S$ be the set of all crossing-free spanning trees of a planar $n$-point set $S$. We prove that ${\cal T}_S$ contains, for each of its members $T$, a length-decreasing sequence of trees $T_o,\ldots,T_k$ such that $T_o=T$, $T_k=MST(S)$, $T_i$ does not cross $T_{i-1}$ for $i=1,\ldots,k$, and $k=O(\log n)$. Here $MST(S)$ denotes the Euclidean minimum spanning tree of the point set $S$. 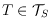As an implication, the number of length-improving and planar edge moves needed to transform a tree $T \in {\cal T}_S$ into $MST(S)$ is only $O(n\log n)$. 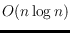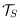Moreover, it is possible to transform any two trees in ${\cal T}_S$ into each other by means of a local and constant-size edge slide operation. Applications of these results to morphing of simple polygons are possible by using a crossing-free spanning tree as a skeleton description of a polygon.

Reference: O. Aichholzer, F. Aurenhammer, and F. Hurtado. Sequences of spanning trees and a fixed tree theorem. Computational Geometry: Theory and Applications, 21(1-2):3-20, 2002. Special Issue. [Report MA2-IR-00-00026, Universitat Politecnica de Catalunya, Barcelona, Spain, 2000].