On Flips in Polyhedral Surfaces

O. Aichholzer, L. Alboul, and F. Hurtado

Abstract:

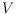
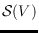
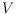
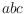
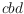
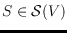
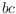
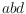
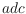
Let $V$ be a finite point set in 3D-space, and let ${\cal S}(V)$ be the set of triangulated polyhedral surfaces homeomorphic to a sphere and with vertex set $V$. Let $abc$ and $cbd$ be two adjacent triangles belonging to a surface $S\in {\cal S}(V)$; the flip of the edge $bc$ would replace these two triangles by the triangles $abd$ and $adc$. The flip operation is only considered when it does not produce a self-intersecting surface. 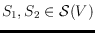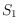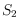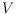In this paper we show that given two surfaces $S_1, S_2\in {\cal S}(V)$, it is possible that there is no sequence of flips transforming $S_1$ into $S_2$, even in the case that $V$ consists of points in convex position.

Reference: O. Aichholzer, L. Alboul, and F. Hurtado. On flips in polyhedral surfaces. In Proc. $17^{th}$ European Workshop on Computational Geometry CG '2001, pages 27-30, Berlin, Germany, 2001.