Edge Operations on Non-Crossing Spanning Trees

O. Aichholzer, F. Aurenhammer, and F. Hurtado

Abstract:

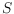
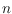
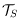
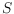
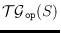
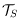
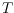
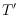
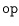
Let $S$ be a set of $n$ points in the Euclidean plane. Consider the set ${\cal T}_S$ of all non-crossing spanning trees of $S$. A tree graph ${\cal TG}_{\tt op}(S)$ is the graph that has ${\cal T}_S$ as its vertex set and that connects vertex (tree) $T$ to vertex $T'$ iff $T' = {\tt op}(T)$, where ${\tt op}$ is some operation that exchanges two tree edges following a specific rule. 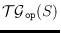The existence of a path between two vertices in ${\cal TG}_{\tt op}(S)$ means transformability of the corresponding trees into each other by repeated application of the operation ${\tt op}$. 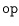The length of a shortest path corresponds to the distance between the two trees with respect to the operation ${\tt op}$. 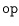Distances of this kind provide a measure of similarity between trees. 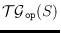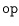We prove new results on ${\cal TG}_{\tt op}(S)$ for two classical operations ${\tt op}$, namely the (improving and crossing-free) edge move and the (crossing-free) edge slide. Applications to morphing of trees and to the continuous deformation of sets of line segments seem reasonable. 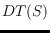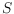Our results mainly rely on a fact of interest in its own right: Let $MST(S)$ and $DT(S)$ be the minimum spanning tree and the Delaunay triangulation of $S$, respectively. 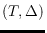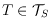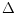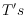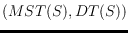Then any pair $(T,\Delta)$, for $T \in {\cal T}_S$ and $\Delta$ being $T's$ constrained Delaunay triangulation, can be transformed into the pair $(MST(S),DT(S))$ via a canonical tree/triangulation sequence.

Reference: O. Aichholzer, F. Aurenhammer, and F. Hurtado. Edge operations on non-crossing spanning trees. In Proc. $16^{th}$ European Workshop on Computational Geometry CG '2000, pages 121-125, Eilat, Israel, 2000.