O. Aichholzer, F. Aurenhammer, P. Gonzalez-Nava, T. Hackl, C. Huemer,
F. Hurtado, H. Krasser, S. Ray, and B. Vogtenhuber
We define general Laman (count) conditions for edges and faces of polygonal
partitions in the plane. Several well-known classes, including
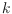
-regular
partitions,
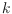
-angulations, and rank
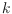
pseudo-triangulations, are shown to
fulfill such conditions. As a consequence non-trivial perfect matchings exist
between the edge sets (or face sets) of two such structures when they live on
the same point set. We also describe a link to spanning tree decompositions
that applies to quadrangulations and certain pseudo-triangulations.