Non-Shellable Drawings of $K_n$ with Few Crossings

B. M. Ábrego, O. Aichholzer, S. Fernández-Merchant, P. Ramos, and B. Vogtenhuber

Abstract:

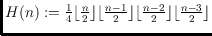
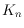
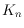
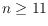
In the early 60s, Harary and Hill conjectured $H(n):=\frac{1}{4}\lfloor\frac{n}{2}\rfloor\lfloor\frac{n-1}{2}\rfloor\lfloor\frac{n-2}{2}\rfloor\lfloor\frac{n-3}{2}\rfloor$ to be the minimum number of crossings among all drawings of the complete graph $K_n$. It has recently been shown that this conjecture holds for so-called shellable drawings of $K_n$. 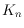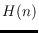For $n \geq 11$ odd, we construct a non-shellable family of drawings of $K_n$ with exactly $H(n)$ crossings. In particular, every edge in our drawings is intersected by at least one other edge. So far only two other families were known to achieve the conjectured minimum of crossings, both of them being shellable.

Reference: B. M. Ábrego, O. Aichholzer, S. Fernández-Merchant, P. Ramos, and B. Vogtenhuber. Non-shellable drawings of $k_n$ with few crossings. In Proc. $26^{th}$ Annual Canadian Conference on Computational Geometry CCCG 2014, page online, Halifax, Nova Scotia, Canada, 2014.