Shellable drawings and the cylindrical crossing number of $K_n$

B. Ábrego, O. Aichholzer, S. Fernández-Merchant, P. Ramos, and G. Salazar

Abstract:

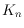
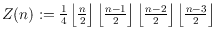
The Harary-Hill Conjecture States that the number of crossings in any drawing of the complete graph $K_n$ in the plane is at least $Z(n):=\frac{1}{4}\left\lfloor \frac{n}{2}\right\rfloor \left\lfloor\frac{n-1}{... ...\left\lfloor \frac{n-2}{2}\right\rfloor\left\lfloor \frac{n-3}{2}\right\rfloor$. In this paper, we settle the Harary-Hill conjecture for shellable drawings. 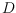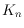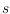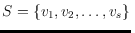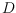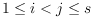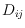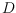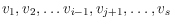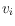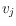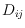We say that a drawing $D$ of $K_n$ is $s$-shellable if there exist a subset $S = \{v_1,v_2,\ldots,v_ s\}$ of the vertices and a region $R$ of $D$ with the following property: For all $1 \leq i < j \leq s$, if $D_{ij}$ is the drawing obtained from $D$ by removing $v_1,v_2,\ldots v_{i-1},v_{j+1},\ldots,v_{s}$, then $v_i$ and $v_j$ are on the boundary of the region of $D_{ij}$ that contains $R$. 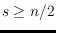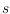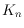For $s\geq n/2$, we prove that the number of crossings of any $s$-shellable drawing of $K_n$ is at least the long-conjectured value Z(n). 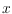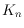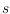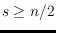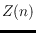Furthermore, we prove that all cylindrical, $x$-bounded, monotone, and 2-page drawings of $K_n$ are $s$-shellable for some $s\geq n/2$ and thus they all have at least $Z(n)$ crossings. The techniques developed provide a unified proof of the Harary-Hill conjecture for these classes of drawings.

Reference: B. Ábrego, O. Aichholzer, S. Fernández-Merchant, P. Ramos, and G. Salazar. Shellable drawings and the cylindrical crossing number of $k_n$. Discrete and Computational Geometry, 52:743-753, 2014.