More on the crossing number of $K_n$: Monotone drawings

B. Ábrego, O. Aichholzer, S. Fernández-Merchant, P. Ramos, and G. Salazar

Abstract:

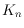
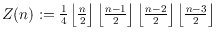
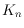
The Harary-Hill conjecture states that the minimum number of crossings in a drawing of the complete graph $K_n$ is $Z(n) :=\frac{1}{4}\left\lfloor \frac{n}{2}\right\rfloor \left\lfloor \frac{n-1... ...left\lfloor \frac{n-2}{2}\right\rfloor \left\lfloor \frac{n-3}{2}\right\rfloor$. This conjecture was recently proved for 2-page book drawings of $K_n$. 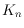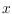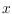As an extension of this technique, we prove the conjecture for monotone drawings of $K_n$, that is, drawings where all vertices have different $x$-coordinates and the edges are $x$-monotone curves.

Reference: B. Ábrego, O. Aichholzer, S. Fernández-Merchant, P. Ramos, and G. Salazar. More on the crossing number of $k_n$: Monotone drawings. Electronic Notes in Discrete Mathematics, 44:411-414, 2013. Special issue dedicated to LAGOS2013.