Computing Balanced Islands in Two Colored Point Sets in the Plane

O. Aichholzer, N. Atienza, J. M. Díaz-Báñez, R. Fabila-Monroy, D. Flores-Peñaloza, P. Pérez-Lantero, J. Urrutia, and B. Vogtenhuber

Abstract:

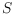
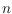
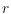
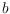
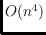
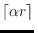
Let $S$ be a set of $n$ points in general position in the plane, $r$ of which are red and $b$ of which are blue. In this paper we present algorithms to find convex sets containing a balanced number of red and blue points. 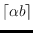We provide an $O(n^4)$ time algorithm that for a given $\alpha \in \left [ 0,\frac{1}{2} \right ]$ finds a convex set containing exactly $\lceil \alpha r\rceil$ red points and exactly $\lceil \alpha b \rceil$ blue points of $S$. 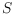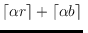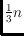If $\lceil \alpha r\rceil+\lceil \alpha b\rceil$ is not much larger than $\frac{1}{3}n$, we improve the running time to $O(n \log n)$. 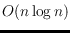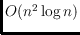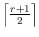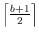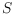We also provide an $O(n^2\log n)$ time algorithm to find a convex set containing exactly $\left \lceil \frac{r+1}{2}\right \rceil$ red points and exactly $\left \lceil \frac{b+1}{2}\right \rceil$ blue points of $S$, and show that balanced islands with more points do not always exist.

Reference: O. Aichholzer, N. Atienza, J. M. Díaz-Báñez, R. Fabila-Monroy, D. Flores-Peñaloza, P. Pérez-Lantero, J. Urrutia, and B. Vogtenhuber. Computing balanced islands in two colored point sets in the plane. Information Processing Letters, 135:28 - 32, 2018.