Bishellable drawings of $K_n$

B. M. Ábrego, O. Aichholzer, S. Fernández-Merchant, D. McQuillan, B. Mohar, P. Mutzel, P. Ramos, R. B. Richter, and B. Vogtenhuber

Abstract:

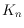
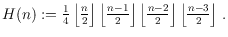
The Harary-Hill conjecture, still open after more than 50 years, asserts that the crossing number of the complete graph $K_n$ is $H(n) := \frac 1 4 \left\lfloor\frac{\mathstrut n}{\mathstrut 2}\right\rfloor ... ...}\right\rfloor \left\lfloor\frac{\mathstrut n-3}{\mathstrut 2}\right\rfloor\,.$ Ábrego et al. [B. M. Ábrego, O. Aichholzer, S. Fernández-Merchant, P. Ramos, and G. Salazar. Shellable drawings and the cylindrical crossing number of $K_n$. 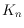Disc. & Comput. 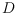Geom., 52(4):743-753, 2014.] introduced the notion of shellability of a drawing $D$ of $K_n$. 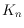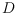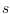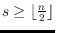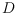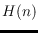They proved that if $D$ is $s$-shellable for some $s\geq\lfloor\frac{n}{2}\rfloor$, then $D$ has at least $H(n)$ crossings. 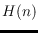This is the first combinatorial condition on a drawing that guarantees at least $H(n)$ crossings. 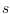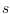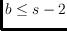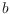In this work, we generalize the concept of $s$-shellability to bishellability, where the former implies the latter in the sense that every $s$-shellable drawing is, for any $b \leq s-2$, also $b$-bishellable. 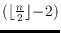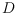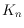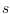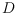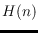Our main result is that $(\lfloor \frac{n}{2} \rfloor\!-\!2)$-bishellability of a drawing $D$ of $K_n$ also guarantees, with a simpler proof than for $s$-shellability, that $D$ has at least $H(n)$ crossings. 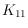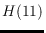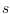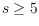We exhibit a drawing of $K_{11}$ that has $H(11)$ crossings, is 3-bishellable, and is not $s$-shellable for any $s\geq5$.This shows that we have properly extended the class of drawings for which the Harary-Hill Conjecture is proved. 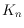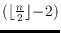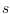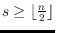Moreover, we provide an infinite family of drawings of $K_n$ that are $(\lfloor \frac{n}{2} \rfloor\!-\!2)$-bishellable, but not $s$-shellable for any $s\geq\lfloor\frac{n}{2}\rfloor$.

Reference: B. M. Ábrego, O. Aichholzer, S. Fernández-Merchant, D. McQuillan, B. Mohar, P. Mutzel, P. Ramos, R. B. Richter, and B. Vogtenhuber. Bishellable drawings of $K_n$. SIAM Journal on Discrete Mathematics, 32(4):2482-2492, 2018.