There is a unique crossing-minimal rectilinear drawing of $K_{18}$

B. Ábrego, O. Aichholzer, S. Fernández-Merchant, J. Leaños, and G. Salazar

Abstract:

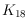
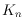
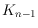
We show that, up to isomorphism, there is a unique crossing-minimal rectilinear drawing of $K_{18}$. As a consequence we settle, in the negative, the following question from Aichholzer and Krasser: does there always exist an crossing-minimal drawing of $K_n$ that contains a crossing-minimal drawing of $K_{n-1}$?

Reference: B. Ábrego, O. Aichholzer, S. Fernández-Merchant, J. Leaños, and G. Salazar. There is a unique crossing-minimal rectilinear drawing of $k_{18}$. In Electronic Notes in Discrete Mathematics, volume 38, pages 547-552, 2011.