Lower and upper bounds on the number of empty cylinders and ellipsoids

O. Aichholzer, F. Aurenhammer, O. Devillers, T. Hackl, M. Teillaud, and B. Vogtenhuber

Abstract:

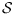
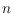
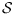
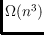
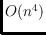
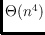
Given a set $\cal S$ of $n$ points in three dimensions, we study the maximum numbers of quadrics spanned by subsets of points in $\cal S$ in various ways. Among various results we prove that the number of empty circular cylinders is between $\Omega(n^3)$ and $O(n^4)$ while we have a tight bound $\Theta(n^4)$ for empty ellipsoids. 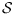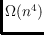We also take interest in pairs of empty homothetic ellipsoids, with application to the number of combinatorially distinct Delaunay triangulations obtained by orthogonal projections of $\cal S$ on a two-dimensional plane, which is $\Omega(n^4)$ and $O(n^5)$. 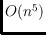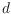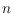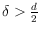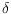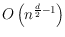A side result is that the convex hull in $d$ dimensions of a set of $n$ points, where one half lies in a subspace of odd dimension  $\delta > \frac{d}{2}$, and the second half is the (multi-dimensional) projection of the first half on another subspace of dimension $\delta$, has complexity only $O\left(n^{\frac{d}{2}-1}\right)$.

Reference: O. Aichholzer, F. Aurenhammer, O. Devillers, T. Hackl, M. Teillaud, and B. Vogtenhuber. Lower and upper bounds on the number of empty cylinders and ellipsoids. In Proc. $25^{th}$ European Workshop on Computational Geometry EuroCG '09, pages 139-142, Brussels, Belgium, 2009.