O. Aichholzer, G. Aloupis, E. Demaine, M. Demaine, S. Fekete,
M. Hoffmann, A. Lubiwk, J. Snoeyink, and a. Winslow
Can folding a piece of paper flat make it larger? In this paper, we explore how
large a shape
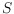
must be scaled to cover a flat-folded copy of itself. We
consider both single folds and arbitrary folded states. The underlying
problem is motivated by computational origami, but also related to other
types of covering problems. In addition to considering special shapes
(squares, equilateral triangles, polygons and disks), we give necessary and
sufficient scaling factors for single folds to convex objects and arbitrary
folds to simply-connected objects.