Convexifying Polygons Without Losing Visibilities

O. Aichholzer, G. Aloupis, E. D. Demaine, M. L. Demaine, V. Dujmovic, F. Hurtado, A. Lubiw, G. Rote, A. Schulz, D. L. Souvaine, and A. Winslow

Abstract:

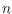
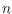
We show that any simple $n$-vertex polygon can be made convex, without losing internal visibilities between vertices, using $n$ moves. Each move translates a vertex of the current polygon along an edge to a neighbouring vertex. In general, a vertex of the current polygon represents a set of vertices of the original polygon that have become co-incident. We also show how to modify the method so that vertices become very close but not co-incident. The proof involves a new visibility property of polygons, namely that every simple polygon has a visibility-increasing edge where, as a point travels from one endpoint of the edge to the other, the visibility region of the point increases.

Reference: O. Aichholzer, G. Aloupis, E. D. Demaine, M. L. Demaine, V. Dujmovic, F. Hurtado, A. Lubiw, G. Rote, A. Schulz, D. L. Souvaine, and A. Winslow. Convexifying polygons without losing visibilities. In Proc. $23^{rd}$ Annual Canadian Conference on Computational Geometry CCCG 2011, pages 229-234, Toronto, Canada, 2011.