Perfect $k$-colored matchings and $k+2$-gonal tilings

O. Aichholzer, L. Andritsch, K. Baur, and B. Vogtenhuber

Abstract:

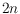
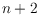
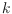
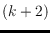
We derive a simple bijection between geometric plane perfect matchings on $2n$ points in convex position and triangulations on $n+2$ points in convex position. We then extend this bijection to monochromatic plane perfect matchings on periodically $k$-colored vertices and $(k+2)$-gonal tilings of convex point sets. These structures are related to Temperley-Lieb algebras and our bijections provide explicit one-to-one relations between matchings and tilings. Moreover, for a given element of one class, the corresponding element of the other class can be computed in linear time.

Reference: O. Aichholzer, L. Andritsch, K. Baur, and B. Vogtenhuber. Perfect $k$-colored matchings and $k+2$-gonal tilings. In Proc. $33^{rd}$ European Workshop on Computational Geometry EuroCG '17, pages 81-84, Malmö, Sweden, 2017.