O. Aichholzer, W. Aigner, F. Aurenhammer, and B. Jüttler
We propose a novel approach for the medial axis approximation of triangulated
solids by using a polyhedral unit ball
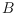
instead of the standard Euclidean
unit ball. By this means, we compute the exact medial axis
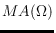
of a
triangulated solid
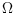
with respect to a piecewise linear (quasi-)metric
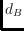
. The obtained representation of
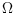
by the medial axis transform
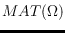
allows for a convenient computation of the trimmed offset of
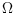
with respect to
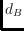
. All calculations are performed within the
field of rational numbers, resulting in a robust and efficient implementation
of our approach. Adapting the properties of
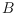
provides an easy way to
control the level of details captured by the medial axis, making use of the
implicit pruning at flat boundary features.