O. Aichholzer, W. Aigner, F. Aurenhammer, T. Hackl, B. Jüttler,
E. Pilgerstorfer, and M. Rabl
We show how to divide the edge graph of a Voronoi diagram into a tree that
corresponds to the medial axis of an (augmented) planar domain. Division into
base cases is then possible, which, in the bottom-up phase, can be merged by
trivial concatenation. The resulting construction algorithm--similar to
Delaunay triangulation methods--is not bisector-based and merely computes
dual links between the sites, its atomic steps being inclusion tests for
sites in circles. This guarantees computational simplicity and numerical
stability. Moreover, no part of the Voronoi diagram, once constructed, has to
be discarded again. The algorithm works for polygonal and curved objects as
sites and, in particular, for circular arcs which allows its extension to
general free-form objects by Voronoi diagram preserving and data saving biarc
approximations. The algorithm is randomized, with expected runtime
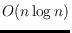
under certain assumptions on the input data. Experiments substantiate an
efficient behavior even when these assumptions are not met. Applications to
offset computations and motion planning for general objects are described.