Straight skeletons of simple polygons

O. Aichholzer, D. Alberts, F. Aurenhammer, and B. Gärtner

Abstract:

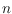
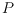
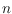
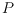
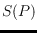
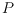
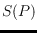
A new internal structure for simple polygons, the straight skeleton, is introduced and discussed. It is a tree and partitions the interior of a given $n$-gon $P$ into $n$ monotone polygons, one for each edge of $P$. Its straight-line structure and its lower combinatorial complexity may make the straight skeleton $S(P)$ preferable to the widely used medial axis of $P$. 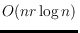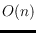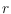We show that $S(P)$ has no Voronoi diagram structure and give an $O(n r \log n)$ time and $O(n)$ space construction algorithm, where $r$ counts the reflex vertices of $P$. 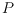As a seemingly unrelated application, the straight skeleton provides a canonical way of constructing a roof of given slope above a polygonal layout of ground walls.

Reference: O. Aichholzer, D. Alberts, F. Aurenhammer, and B. Gärtner. Straight skeletons of simple polygons. In Proc. $4^{th}$ Int. Symp. of LIESMARS, pages 114-124, Wuhan, P. R. China, 1995.