A novel type of skeleton for general polygonal figures, the straight skeleton
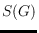
of a planar straight line graph
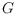
, is introduced and discussed.
Exact bounds on the size of
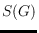
are derived. The straight line structure
of
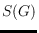
and its lower combinatorial complexity may make
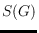
preferable
to the widely used Voronoi diagram (or medial axis) of
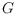
in several
applications. We explain why
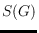
has no Voronoi diagram based
interpretation and why standard construction techniques fail to work. A
simple
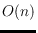
space algorithm for constructing
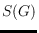
is proposed. The
worst-case running time is
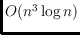
, but the algorithm can be expected
to be practically efficient, and it is easy to implement. We also show that
the concept of
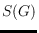
is flexible enough to allow an individual weighting of
the edges and vertices of
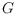
, without changes in the maximal size of
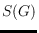
,
or in the method of construction. Apart from offering an alternative to
Voronoi-type skeletons, these generalizations of
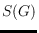
have applications to
the reconstruction of a geographical terrain from a given river map, and to
the construction of a polygonal roof above a given layout of ground walls.