We consider hyperplanes spanned by vertices of the unit
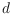
-cube. We classify
these hyperplanes by parallelism to coordinate axes, by symmetry of the
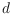
-cube vertices they avoid, as well as by so-called hull-honesty.
(Hull-honest hyperplanes are those whose intersection figure with the
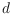
-cube coincides with the convex hull of the
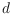
-cube vertices they
contain; they do not cut
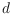
-cube edges properly.) We describe relationships
between these classes, and give the exact number of hull-honest hyperplanes,
in general dimensions. An experimental enumeration of all spanned hyperplanes
up to dimension eight showed us the intrinsic difficulty of developing a
general enumeration scheme. Motivation for considering such hyperplanes stems
from coding theory, from linear programming, and from the theory of machine
learning.