For a planar point set
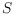
let
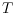
be a triangulation of
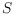
and
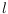
a line
properly intersecting
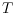
. We show that there always exists a unique path in
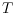
with certain properties with respect to
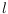
. This path is then
generalized to (non triangulated) point sets restricted to the interior of
simple polygons. This so-called triangulation path enables us to treat
several triangulation problems on planar point sets in a divide &
conquer-like manner. For example, we give the first algorithm for counting
triangulations of a planar point set which is observed to run in time
sublinear in the number of triangulations. Moreover, the triangulation path
proves to be useful for the computation of optimal triangulations.