In this paper we study local properties of two well known triangulations of a
planar point set
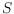
, both of which are defined in a non-local way. The first
one is the greedy triangulation (GT) that is defined procedurally: it can be
obtained by starting with the empty set and at each step adding the shortest
compatible edge between two points of
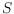
, where a compatible edge is defined
to be an edge that does not cross any of the previously inserted edges. The
other triangulation we deal with is the minimum-weight triangulation (MWT)
which minimizes the sum of the length of the edges among all possible
triangulations of
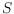
. We present several results on exclusion- and
inclusion-regions for these two triangulations.