In dieser Arbeit werden affine Hyperebenen in höherdimensionalen Räumen
behandelt, die den
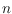
-dimensionalen Hyperkubus schneiden. Dabei konzentriert
sich die Untersuchung auf folgende Fragestellung: Wieviele und welche Arten
von Hyperebenen gibt es, die durch Eckpunkte des Hyperkubus eindeutig
festgelegt sind? Neben der Betrachtung, wieviele solcher Hyperebenen
existieren, wird eine Klassifizierung nach verschiedenen Kriterien wie
Symmetrie, Parallelität zu den Koordinatenachsen, Anzahl der
geschnittenen Eckpunkte etc. untersucht. Die Arbeit enthält sowohl eine
vollständige enumerative Berechnung aller relevanten Werte bis
einschließlich der achten Dimension, als auch die theoretische Herleitung
allgemein gültiger Sätze über solche Hyperebenen. Die
Beiträge dieser Arbeit fallen in das Gebiet der geometrischen
Kombinatorik und finden sowohl in der Codierungs- und Lerntheorie als auch in
der linearen Optimierung sowie im VLSI-Design Anwendung.