Extremal Properties of 0/1-Polytopes of Dimension 5

O. Aichholzer

Abstract:

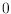
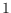
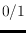
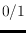
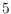
In this paper we consider polytopes whose vertex coordinates are $0$ or $1$, so called $0/1$-polytopes. For the first time we give a complete enumeration of all $0/1$-polytopes of dimension $5$, which enables us to investigate various of their combinatorial extremal properties.
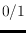
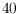
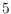
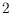
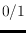
For example we show that the maximum number of facets of a five-dimensional $0/1$-polytope is $40$, answering an open question of Ziegler. Based on the complete enumeration for dimension $5$ we obtain new results for $2$-neighbourly $0/1$-polytopes for higher dimensions.

Reference: O. Aichholzer. Extremal properties of 0/1-polytopes of dimension 5. In G. Ziegler and G. Kalai, editors, Polytopes - Combinatorics and Computation, pages 111-130. Birkhäuser, 2000. [SFB-Report F003-132, TU Graz, Austria, 1998].