[Empty] [colored] $k$-gons - Recent results on some Erdös-Szekeres type problems

O. Aichholzer

Abstract:

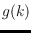
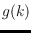
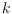
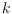
We consider a family of problems which are based on a question posed by Erdos and Szekeres in 1935: “What is the smallest integer $g(k)$ such that any set of $g(k)$ points in the plane contains at least one convex $k$-gon?” In the mathematical history this has become well known as the “Happy End Problem”. There are several variations of this problem: The $k$-gons might be required to be empty, that is, to not contain any points of the set in their interior. 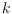In addition the points can be colored, and we look for monochromatic $k$-gons, meaning polygons spanned by points of the same color. 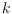Beside the pure existence question we are also interested in the asymptotic behavior, for example whether there are super-linear many $k$-gons of some type. 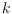And finally, for several of these problems even small non-convex $k$-gons are of interest. We will survey recent progress and discuss open questions for this class of problems.

Reference: O. Aichholzer. [Empty] [colored] $k$-gons - Recent results on some Erdös-Szekeres type problems. In Proc. XIII Encuentros de Geometría Computacional, pages 43-52, Zaragoza, Spain, 2009.