The central topic of this thesis is the
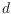
-dimensional hypercube (
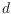
-cube).
Despite of its simple definition, the
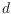
-cube has been an object of study
from various points of view. The contributions of this thesis are twofold. In
the combinatorial part we investigate the structure of hyperplanes
intersecting the
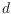
-cube: How many and which types of hyperplanes can be
spanned by vertices of the
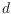
-cube? What is the minimum number of skew
hyperplanes that cover all the vertices of the
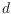
-cube? What is the best
arrangement of slicing hyperplanes to linearly separate all neighbours on the
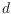
-cube? Such results are then used e.g. for determining the maximal number
of facets a 5-dimensional
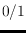
-polytope can achieve. In the second part of
the thesis we consider algorithmical properties of the
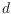
-cube. We first
obtain efficient clustering methods for objects represented as binary strings
of fixed length
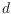
, including various agglomerative hierarchical methods
like single linkage and complete linkage. Utilizing these hierarchical
structures we derive a new efficient approach to the
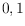
-string searching
problem, where for a given set of binary strings of fixed length
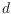
and a
query string one asks for the most similar string in this set. Motivation for
investigating these problems stems, among other areas, from coding theory,
communication theory, and learning theory.