Rainbow polygons for colored point sets in the plane

D. Flores-Peñaloza, M. Kano, L. Martínez-Sandoval, D. Orden, J. Tejel, C. D. Tóth, J. Urrutia, and B. Vogtenhuber

Abstract:

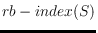
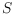
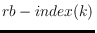
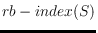
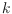
Given a colored point set in the plane, a perfect rainbow polygon is a simple polygon that contains exactly one point of each color, either in its interior or on its boundary. 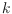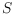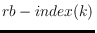Let $\operatorname{rb-index}(S)$ denote the smallest size of a perfect rainbow polygon for a colored point set $S$, and let $\operatorname{rb-index}(k)$ be the maximum of $\operatorname{rb-index}(S)$ over all $k$-colored point sets in general position; that is, every $k$-colored point set $S$ has a perfect rainbow polygon with at most $\operatorname{rb-index}(k)$ vertices. 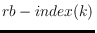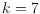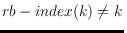In this paper, we determine the values of $\operatorname{rb-index}(k)$ up to $k=7$, which is the first case where $\operatorname{rb-index}(k)\neq k$, and we prove that for $k\ge 5$,

$$\frac{40\lfloor (k-1)/2 \rfloor -8}{19} \leq\operatorname{rb-index}(k)\leq 10 \bigg\lfloor\frac{k}{7}\bigg\rfloor + 11.$$

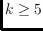
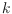
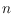
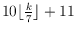
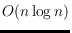
Furthermore, for a $k$-colored set of $n$ points in the plane in general position, a perfect rainbow polygon with at most $10 \lfloor\frac{k}{7}\rfloor + 11$ vertices can be computed in $O(n\log n)$ time.

Reference: D. Flores-Peñaloza, M. Kano, L. Martínez-Sandoval, D. Orden, J. Tejel, C. D. Tóth, J. Urrutia, and B. Vogtenhuber. Rainbow polygons for colored point sets in the plane. Discrete Mathematics, 344(7):112406, 2021.