Towards Crossing-Free Hamiltonian Cycles in Simple Drawings of Complete Graphs

O. Aichholzer, J. Orthaber, and B. Vogtenhuber

Abstract:

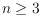
It is a longstanding conjecture that every simple drawing of a complete graph on $n\geq 3$ vertices contains a crossing-free Hamiltonian cycle. We strengthen this conjecture to there exists a crossing-free Hamiltonian path between each pair of vertices and show that this stronger conjecture holds for several classes of simple drawings, including strongly c-monotone drawings and cylindrical drawings. As a second main contribution, we give an overview on different classes of simple drawings and investigate inclusion relations between them up to weak isomorphism.

Reference: O. Aichholzer, J. Orthaber, and B. Vogtenhuber. Towards crossing-free hamiltonian cycles in simple drawings of complete graphs. Computing in Geometry and Topology, 3(2):5:1-5:30, Jan. 2024.