In their seminal work on Multidimensional Sorting, Goodman and Pollack
introduced the so-called order type, which for each ordered triple of a point
set in the plane gives its orientation, clockwise or counterclockwise. This
information is sufficient to solve many problems from discrete geometry where
properties of point sets do not depend on the exact coordinates of the points
but only on their relative positions. Goodman and Pollack showed that an
efficient way to store an order type in a matrix
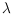
of quadratic size
(w.r.t. the number of points) is to count for every oriented line spanned by
two points of the set how many of the remaining points lie to the left of
this line. We generalize the concept of order types to bicolored point sets
(every point has one of two colors). The bicolored order type contains the
orientation of each bicolored triple of points, while no information is
stored for monochromatic triples. Similar to the uncolored case, we store the
number of blue points that are to the left of an oriented line spanned by two
red points or by one red and one blue point in
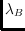
. Analogously the
number of red points is stored in
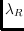
. As a main result, we show that
the equivalence of the information contained in the orientation of all
bicolored point triples and the two matrices
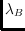
and
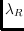
also
holds in the colored case. This is remarkable, as in general the bicolored
order type does not even contain sufficient information to determine all
extreme points (points on the boundary of the convex hull of the point set).
We then show that the information of a bicolored order type is sufficient to
determine whether the two color classes can be linearly separated and how one
color class can be sorted around a point of the other color class. Moreover,
knowing the bicolored order type of a point set suffices to find bicolored
plane perfect matchings or to compute the number of crossings of the complete
bipartite graph drawn on a bicolored point set in quadratic time.